Abstract
Objective
The Radford nomogram, an old mathematical chart device to estimate the required ventilation for maintaining normocapnia, remains unvalidated in patients undergoing modern, balanced anesthesia. This study aims to investigate the performance of the Radford nomogram in patients undergoing general anesthesia and derive a simple equation to estimate the minute volume required to attain normocapnia (MVnorm).
Methods
This single-center retrospective study enrolled 78 patients (age ≥ 18 years) undergoing cerebral revascularization for Moyamoya disease. We defi ned MVnorm as the median of all values of the minute volume during normocapnia (estimated PaCO2: 38–42 mmHg). We examined the agreement level between the estimated minute volume using the Radford nomogram and MVnorm using the Bland–Altman analysis. Furthermore, we developed and validated a simple equation predicting MVnorm based on gender and a multiple of body weight, using a split-sample validation technique.
Result
The Radford nomogram tended to overestimate MVnorm with a mean bias of 560 mL/min (95% limits of agreement, -848–1,968 mL/min). The equation developed using data from the development group (n = 52): required minute volume (mL/min) = 85 × body weight (kg) in male patients and 70 × body weight (kg) in female patients. In the validation group (n = 26), the mean bias of this simple equation was 224 mL/min (95% limits of agreement, -1,264–1,712 mL/min).
Conclusion
The Radford nomogram overestimates MVnorm in modern, balanced anesthesia. The simple equation using gender and a multiple of body weight yields similar predictive performance to the Radford nomogram.
Introduction
Goal of intraoperative ventilation was to provide normocapnia for patients at risk of cerebral ischemia such as those with Moyamoya disease.1 Hypocapnia causes cerebral vasoconstriction and could result in cerebral ischemia.2,3 Alternatively, hypercapnia might cause a decline in the cerebral blood fl ow by “intracerebral steal” because the collateral network of vessels is in a state of maximal vasodilation.4-6
In practice, however, measuring the partial pressure of arterial carbon dioxide (PaCO2) and attaining normocapnia in real time is challenging, especially immediately after anesthesia induction. Repeated assessment of arterial blood gas is diffi cult immediately after anesthesia induction because anesthesiologists are preoccupied with several tasks such as airway management, blood pressure regulation, and patient positioning. Although the partial pressure of end-tidal carbon dioxide (PetCO2) has been used as a noninvasive and real-time estimate of PaCO2, regulating the ventilation using PetCO2 as an indicator might lead to unintended hyperventilation or hypoventilation because of marked variability in the difference between PaCO2 and PetCO2 in mechanically ventilated patients.7-9 Thus, estimating the required minute ventilation to attain normocapnia would be useful to ascertain the initial ventilator settings, minimizing the risk of hyperventilation or hypoventilation.
The Radford nomogram10 is an old mathematical chart device to predict necessary tidal volume for mechanical ventilation on the basis of gender, body weight, and respiratory rate. Although the nomogram was validated in patients undergoing general anesthesia in the 1960,11 the respiratory requirement might be different in patients undergoing modern, balanced anesthesia.
Hence, the primary objective of this study is to investigate the performance of the Radford nomogram in patients undergoing cerebral revascularization for Moyamoya disease, by correlating the minute volume estimated using the Radford nomogram (MVrad) with the measured minute volume required to attain normocapnia (MVnorm). The secondary objective of this study is to derive a simple equation to predict MVnorm.
Methods
Study Design, Setting, and Population
This single-center retrospective study was conducted in Kyoto University Hospital, a teaching hospital in Japan. This study protocol was approved by the Institutional Review Board approved (approval number: R1542, May 17, 2018), which waived the requirement for obtaining informed consent. This study was conducted in accordance with Declaration of Helsinki (2013) and relevant laws in Japan. This study adheres to the Guidelines for Reporting Reliability and Agreement Studies.12
In this study, we enrolled adult (age: ≥ 18 years) patients who underwent cerebral revascularization for Moyamoya disease at Kyoto University Hospital from April 2008 to March 2018. We excluded patients if their intraoperative ventilator settings were missing or normocapnia was not attained throughout the surgery because MVnorm could not be calculated for them. For patients who had > 1 surgery that met the eligibility criteria, we included only the first surgery performed on the patient. All enrolled patients underwent general anesthesia and tracheal intubation. General anesthesia was induced with propofol and remifentanil, while tracheal intubation was facilitated by rocuronium. Anesthesia was maintained with sevoflurane or propofol combined with remifentanil and rocuronium. After tracheal intubation, patients were ventilated using Fabius GS premium (Dräger Medical, Lübeck, Germany). Furthermore, ventilator setting was adjusted targeting normocapnia (PaCO2 measured by arterial blood gas analysis: 38–42 mmHg).
Data Collection
At our institution, the electronic database of surgical patients comprised data on age, gender, height, weight, the American Society of Anesthesiologists Physical Status, duration of surgery, and intraoperative blood loss. Moreover, we collected data on smoking history (ever smoker was defined as smoking ≥ 100 cigarettes during lifetime up to the surgery, as reported previously13-15), diagnosis of chronic pulmonary disease (defined as a previous diagnosis of chronic obstructive pulmonary disease, chronic bronchitis, or emphysema), history of asthma, and ventilatory parameters and arterial blood gas results during the surgery from the electronic medical record system.
Calculating the Minute Volume Required to Attain Normocapnia
The ventilatory settings (tidal volume, respiratory rate, and minute volume) and PetCO2 values were recorded automatically every minute directly into an anesthesia information management system (PrimeGaia PRM-7500, Nihon Kohden, Tokyo, Japan). We calculated the estimated PaCO2 as follows: (1) defining the arterial to end-tidal partial pressure difference of carbon dioxide (Pa-etCO2) for each individual patient as the median of differences between PaCO2 and simultaneous PetCO2 readings (PaCO2–PetCO2) for all intraoperative arterial blood gas measurements, and (2) calculating the estimated PaCO2 by adding Pa-etCO2 to PetCO2 value recorded every minute. Then, we defined normocapnia as estimated PaCO2 of 38–42 mmHg. We considered the median of all values of the minute volume during normocapnia as MVnorm.
Prediction of the Minute Volume Required to Attain Normocapnia Using the Radford Nomogram
We applied the Radford nomogram, a mathematical chart device to predict necessary tidal volume for mechanical ventilation on the basis of gender, body weight, and respiratory rate, to each patient and estimated the tidal volume required to atttain normocapnia (TVrad) for a breathing frequency of 12 breaths/ min. Then, we calculated MVrad as 12 × TVrad. We also calculated the minute volumes required to attain normocapnia using the Radford nomogram for breathing frequencies of 10 and 14 breaths/min (MVrad10 and MVrad14, respectively), and assessed the agreement of MVrad10 or MVrad14 with MVnorm using Bland–Altman analysis.
Statistical Analyses
In this study, continuous data are presented as median [interquartile range], while categorical variables as number (%). We used the linear regression analysis to estimate the correlation between continuous variables. In addition, the agreement between the predicted minute volume and MVnorm was displayed graphically on the Bland–Altman plots and was presented by the mean difference between the two measurements and the 95% limits of agreement, representing the differences likely to arise between the two measurements with a 95% probability. We verified the assumption of the normal distribution of the difference using the Kolmogorov–Smirnov normality test. Moreover, we assessed the proportion of patients whose predicted minute volumes were above or below MVnorm by, at least, 10% to quantify the extent to which the predicting method was either overestimating or underestimating MVnorm.
We derived a simple equation to predict MVnorm based on the average values of MVnorm per kg body weight for men and women. The estimated minute volume using this simple equation was designated as MVsimp. We also derived an equation using the ideal body weight rather than actual body weight because, in our opinion, the equation using the actual body weight might overestimate MVnorm in obese patients. We determined the ideal body weight using the body mass index method.16 The estimated minute volume based on gender and ideal body weight was designated as MVsimp-IBW. Additionally, we examined whether smoking status and/or history of asthma were associated with MVnorm per kg body weight independent of gender, using multivariable linear regression analysis with MVnorm per kg body weight as a dependent variable. We used a split-sample validation technique for equation development and validating. We derived equations based on the data obtained from two-thirds of the study population randomly selected using the simple random sampling procedure, and then, verified the equations on the remaining one-third of patients.
We did not conduct a formal sample size calculation because this study did not aim to test a certain hypothesis but assess the agreement between the estimated and measured minute volume. Instead, all eligible surgeries performed from the introduction of the current anesthesia information management system (PrimeGaia PRM-7500) at our institution to the conception of this study were included to maximize the reliability of our results. All statistical tests in this study were two-tailed, and we considered p < 0.05 as statistically significant. All statistical analyses were performed using the statistical program R (available at http://cran.r-project.org).
Results
The electronic database search of surgical patients at our institution yielded 134 cerebral revascularization surgeries for Moyamoya disease. After excluding 27 surgeries because of missing intraoperative ventilator settings, 3 for not attaining normocapnia, and 26 for not being the first surgery performed on the patient, we included 78 surgeries in this study.
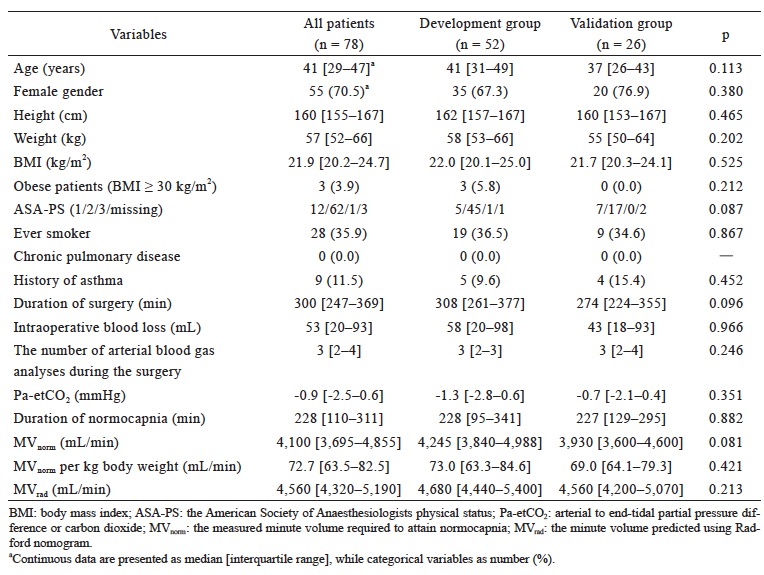
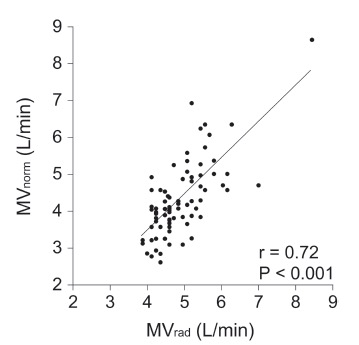
Table 1 summarizes patients’ characteristics and operative variables. Study participants were aged 18–67 years, and 70.5% were females. No patient had chronic pulmonary disease. MVnorm ranged 2,640– 8,680 (median, 4,100) mL/min, and MVnorm per kg body weight ranged 47.7–115.2 (median, 72.7) mL/ min. In addition, MVrad ranged 3,840–8,400 (median, 4,560) mL/min. The linear regression analysis revealed a significant and positive correlation between MVrad and MVnorm (Pearson’s correlation coefficient: 0.72; p < 0.001; Fig. 1). The Bland–Altman analysis revealed that MVrad tends to overestimate MVnorm with a mean bias of 560 (standard deviation, 718) mL/min; 95% limits of agreement ranged from -848 to 1,968 mL/min (Fig. 2). The proportion of cases whose prediction fell within ±10% of MVnorm was 30.8%; MVrad overestimated MVnorm by > 10% in 47 patients (60.3%), and underestimated by > 10% in seven patients (9.0%). We also assessed the agreement of MVrad10 or MVrad14 with MVnorm and found that both MVrad10 and MVrad 14 tend to overestimate MVnorm (mean bias, 400 and 255 mL; standard deviation, 700 and 707 mL/min; respectively).
Download full-size image
Download full-size image
Download full-size image
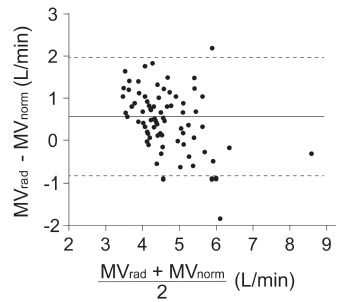
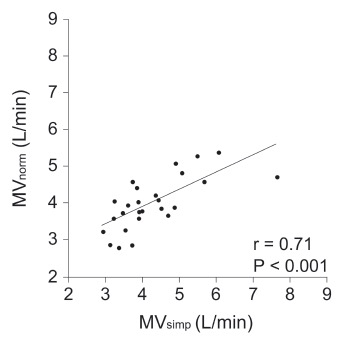
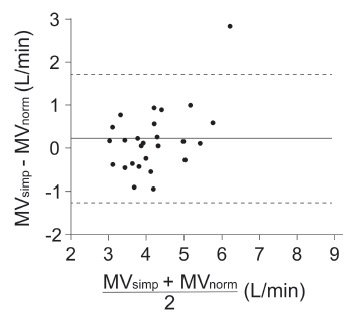
Then, we derived a simple equation estimating MVnorm using gender and a multiple of body weight. In the development dataset (n = 52), MVnorm per kg body weight was significantly higher in male patients (average: 84.5 vs. 69.7 mL/min per kg body weight; p < 0.001, Student’s t-test). Based on these findings, we derived following equation: MVsimp (mL/min) = 85 × body weight (kg) for males and MVsimp (mL/min) = 70 × body weight (kg) for females. The linear regression analysis using the validation dataset (n = 26) revealed a significant and positive correlation between MVsimp and MVnorm (Pearson’s correlation coefficient: 0.71; p < 0.001; Fig. 3). The Bland–Altman analysis indicated that MVsimp estimates MVnorm with a mean bias of 224 (standard deviation, 759) mL/min; 95% limits of agreement ranged from -1,264 to 1,712 mL/min (Fig. 4). The proportion of cases whose prediction fell within ±10% of MVnorm was 50.0%; MVsimp overestimated MVnorm by > 10% in eight patients (30.8%) and underestimated by > 10% in five patients (19.2%).
Download full-size image
Download full-size image
Furthermore, we derived an equation estimating MVnorm based on gender and ideal body weight. The mean MVnorm per kg ideal body weight was 89.4 mL/min in males and 71.5 mL/min in females in the developing dataset. Thus, we derived following equation: MVsimp-IBW (mL/min) = 90 × ideal body weight (kg) for males and MVsimp-IBW (mL/min) = 70 × ideal body weight (kg) for females. We observed a significant and positive correlation between MVsimp-IBW and MVnorm in the validation dataset (Pearson’s correlation coefficient: 0.78; p < 0.001). The Bland–Altman analysis revealed that MVsimp-IBW estimates MVnorm with a mean bias of 269 (standard deviation, 582) mL/min; 95% limits of agreement ranged from -872 to 1,410 mL/min. Using the ideal body weight rather than the actual body weight did not significantly increase the percentage of cases whose prediction fell within ±10% of MVnorm (50% vs. 50%; p = 1.000).
In multivariable linear regression analysis with MVnorm per kg body weight as a dependent variable, neither smoking status nor history of asthma was significantly associated with MVnorm per kg body weight (Table 2).

Download full-size image
Discussion
This study investigated the performance of the Radford nomogram to estimate the minute volume required to attain normocapnia in patients undergoing cerebral revascularization for Moyamoya disease. The findings revealed that the Radford nomogram overestimated the required minute volume with a mean bias of 560 mL/min. In addition, we derived and validated a simple equation using gender and a multiple of body weight to estimate the required minute volume.
Nunn11 reported that the Radford nomogram displayed little systematic error in patients undergoing general anesthesia. In this study, however, the Radford nomogram overestimated MVnorm by 560 mL/ min on average, and overestimation exceeded 10% in 60.3% of patients. These findings suggest that patients are prone to be hyperventilated when determining the ventilator setting based on the Radford nomogram. Several possible descriptions exist for the discrepancy in the findings of Nunn11 and this study. First, drugs used for anesthesia in this study (propofol/sevoflurane and remifentanil) are, perhaps, markedly different from those when Nunn11 conducted their study. The difference in anesthetic drugs could have accounted for the differences in the metabolic activity and carbon dioxide production. Second, the difference in the ventilators used could have led to the difference in the size of dead space or the efficiency of ventilation. Third, the validation methods for the Radford nomogram varied between studies. Nunn11 obtained data from anesthetized patients with various PaCO2 values and used the scatter plot of PaCO2 against the minute volume. Conversely, we used data from patients who attained normocapnia. To the best of our knowledge, this is the first study to investigate the performance of the Radford nomogram using data from anesthetized patients who attained normocapnia.
We derived the simple equation using gender and a multiple of body weight as a practical equation to estimate the required minute volume; it had smaller mean bias and the similar width of limits of agreement compared with the Radford nomogram. Moreover, it offers an advantage of being easy to remember, which is essential for practical use. Ascertaining the initial ventilator setting using our simple equation and then adjusting it per the blood gas results could effectively minimize the risk of hypercapnia or hypocapnia.
Ocbo and Terry17 proposed a simple formula to estimate the ventilatory requirement in anesthetized patients—a minute volume of 84–88 mL/min per kg body weight. However, in our dataset, MVnorm per kg body weight was significantly higher in male patients than that in female patients. Thus, we derived the equation separately for male and female patients.
In our dataset, using the ideal body weight rather than the actual body weight did not markedly improve the agreement between the predicted minute volume and MVnorm. However, our dataset comprised only three (3.8%) obese patients (body mass index ≥ 30 kg/m2). Hence, we could not determine which one of the equations based on the actual or ideal body weight precisely predicts the required minute volume in obese patients, thereby necessitating future studies.
Strengths and Limitations
The strengths of this study included the precise estimation of the minute volume required to attain normocapnia by calculating the estimated PaCO2 on the minute-by-minute basis. Conversely, this study has several limitations that merit consideration when interpreting the results. First, we enrolled only relatively young patients (all patients were aged < 70 years) and did not include patients with chronic pulmonary diseases. The minute volume required to attain normocapnia might be different in older patients or those with chronic pulmonary diseases. Hence, future studies are warranted to ascertain the optimal initial ventilator settings in these patients. Second, ventilatory strategies to attain normocapnia were not standardized, and the variation in the ventilatory strategies might have affected our results. Finally, the small sample size might have reduced the reliability of our results.
Conclusion
This study reveals that the Radford nomogram overestimates the minute volume required to attain normocapnia with a mean bias of 560 mL/min in modern, balanced anesthesia. We propose the following simple equation to estimate the required minute volume: required minute volume (mL/min) = 85 × body weight (kg) in male patients and 70 × body weight (kg) in female patients.
Acknowledgments
This work was supported, in part, by JSPS KAKENHI (grant number: 16K20092, principal investigator: Toshiyuki Mizota; grant number: 17K16728, principal investigator: Hiroshi Fukagawa).
References
| 1 |
Chui J, Manninen P, Sacho RH, Venkatraghavan L.
Anesthetic management of patients undergoing intracranial bypass procedures.
Anesth Analg 2015;120:193–203.
|
| 2 | |
| 3 |
Baykan N, Özgen S, Ustalar ZS, Dağçinar A, Özek MM.
Moyamoya disease and anesthesia.
Paediatr Anaesth 2005;15:1111–1115.
|
| 4 |
Kurehara K, Ohnishi H, Touho H, Furuya H, Okuda T.
Cortical blood flow response to hypercapnia during anaesthesia in Moyamoya disease.
Can J Anaesth 1993;40:709–713.
|
| 5 |
Iwama T, Hashimoto N, Yonekawa Y.
The relevance of hemodynamic factors to perioperative ischemic complications in childhood moyamoya disease.
Neurosurgery 1996;38:1120–1125.
|
| 6 |
Yusa T, Yamashiro K.
Local cortical cerebral blood flow and response to carbon dioxide during anesthesia in patients with moyamoya disease.
J Anesth 1999;13:131–135.
|
| 7 |
Russel l GB, Graybeal JM.
End-tidal carbon dioxide as an indicator of arterial carbon dioxide in neurointensive care patients.
J Neurosurg Anesthesiol 1992;4:245–249.
|
| 8 |
Isert PR.
Arterial to end-tidal carbon dioxide differences during neurosurgical procedures.
Can J Anaesth 1996;43:196–197.
|
| 9 |
Mackersie RC, Karagianes TG.
Use of end-tidal carbon dioxide tension for monitoring induced hypocapnia in head-injured patients.
Crit Care Med 1990;18:764–765.
|
| 10 |
Radford EP Jr.
Ventilation standards for use in artificial respiration.
J Appl Physiol 1955;7:451–460.
|
| 11 |
Nunn JF.
Prediction of carbon dioxide tension during anaesthesia.
Anaesthesia 1960;15:123–133.
|
| 12 |
Kottner J, Audigé L, Brorson S, et al.
Guidelines for Reporting Reliability and Agreement Studies (GRRAS) were proposed.
J Clin Epidemiol 2011;64:96–106.
|
| 13 |
Chen J, Qi Y, Wampfler JA, et al.
Effect of cigarette smoking on quality of life in small cell lung cancer patients.
Eur J Cancer 2012;48:1593–1601.
|
| 14 |
Kawaguchi T, Matsumura A, Fukai S, et al.
Japanese ethnicity compared with Caucasian ethnicity and never-smoking status are independent favorable prognostic factors for overall survival in non-small cell lung cancer: a collaborative epidemiologic study of the National Hospital Organization Study Group for Lung Cancer (NHSGLC) in Japan and a Southern California Regional Cancer Registry databases.
J Thorac Oncol 2010;5:1001–1010.
|
| 15 |
Tao ML, Guo MD, Weiss R, et al.
Smoking in adult survivors of childhood acute lymphoblastic leukemia.
J Natl Cancer Inst 1998;90:219–225.
|
| 16 |
Lemmens HJ, Brodsky JB, Bernstein DP.
Estimating ideal body weight—a new formula.
Obes Surg 2005;15:1082–1083.
|
| 17 |
Ocbo EM, Terry RN.
Proposed formula for ventilatory requirements in apneic anesthetized patients.
Anesth Analg 1969;48:455–460.
|